This code uses TensorFlow to simulate a physical system. The novel thing about the code is that the only physics you need to specify is the Hamiltonian. The rest is automatically determined by automatic differentiation. In other words if you can specify the Hamiltonian using canonical coordinates then the code will generate and numerically (RK4) solve the equations of motion:

\[\frac{\mathrm{d}\boldsymbol{p}}{\mathrm{d}t} = -\frac{\partial \mathcal{H}}{\partial \boldsymbol{q}}\quad,\quad \frac{\mathrm{d}\boldsymbol{q}}{\mathrm{d}t} = +\frac{\partial \mathcal{H}}{\partial \boldsymbol{p}}\]

Below is a simulation of a vibrating string (modeled as 100 masses connected linearly by springs) generated using the code.

Here is the code simulating a double pendulum:

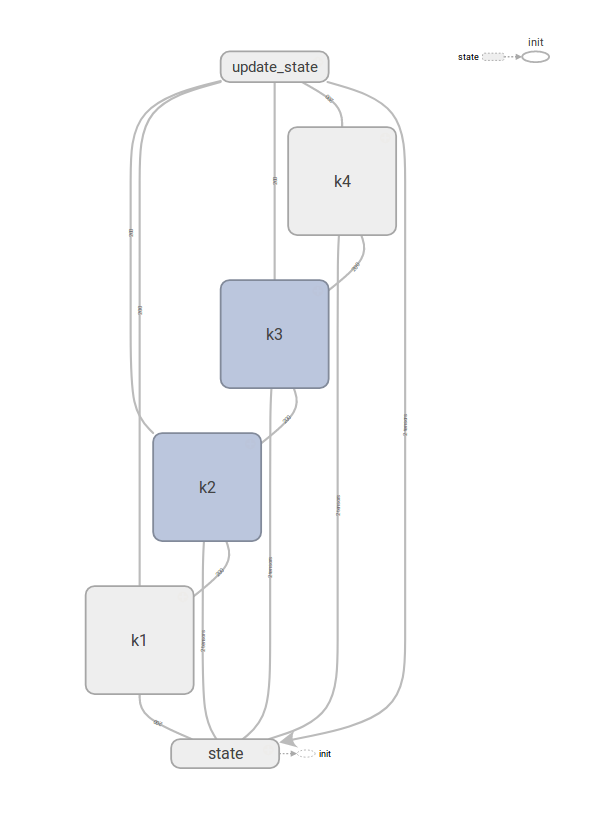
Below is a visualization of the TensorFlow graph. You can see the four boxes responsible for calculating the four k values of fourth order Runge-Kutta method and how they are then combined into the update_state box.